D&D Simple Creature Loot
This is the last of this run of articles on the new tables that I made for my latest DM screen but it's actually the first thing that I started tampering around last August: treasure you might find on a slain monster.
I already tried to simplify the tables found on DMG136 (see Dungeon Master Tables (and Tall Tales)) but felt the mechanics could be simplified too by reducing the number of die rolls required just to get to a value of an individual creature's personal wealth.
The second part, the type of loot, came from my in-game experience of trying to think of something the recently deceased NPCs had of value; repetitive coin pouches were just, well, repetitive.
| CR | 3d6 | on a double or triple 1-3 | on a double or triple 4-5 | on a double or triple 6 |
|---|---|---|---|---|
| 0-4 | CP | EP +1d6 GP | +1d6 GP | +1d6 PP |
| 5-10 | EP x10 | +3d6 PP | +1d6 PP | PP +3d6 PP |
| 11-16 | PP x10 | PP x10 | PP x4 | PP x3 |
| 17+ | PP x100 | PP x50 | PP x40 | PP x30 |
| Mundane loot | (3d6) | Fancy items (on a double or triple) |
|---|---|---|
| Coin | 1 | Jewellery |
| Gems | 2 | Furniture |
| Supplies | 3 | Tools |
| Food | 4 | Musical instrument |
| Drink | 5 | Perfume or spices |
| Art | 6 | Cloth or clothes |
The Method

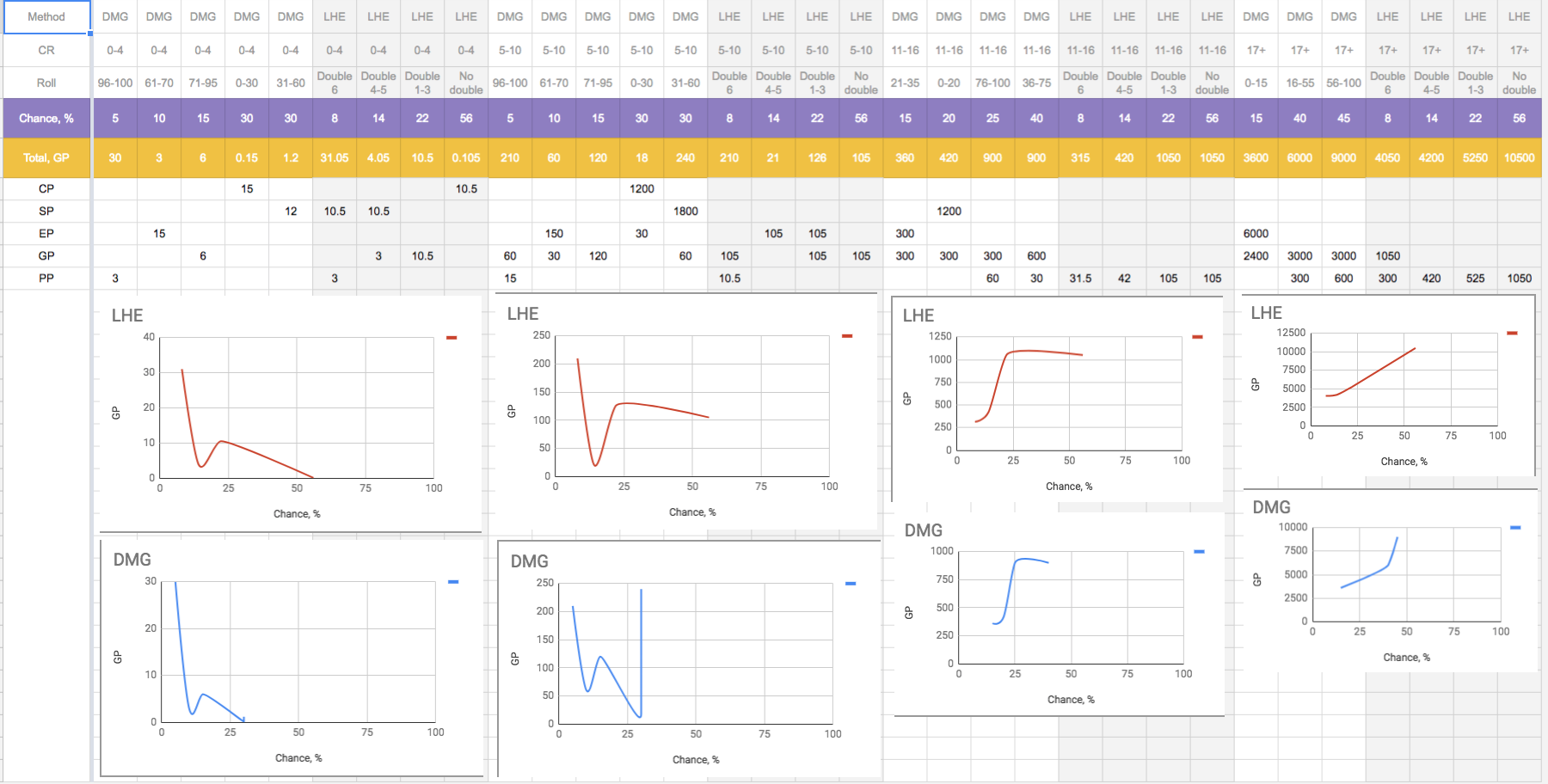
I started by dissecting the DMG rules in my notebook, normalising the values to a gold (GP) standard, then plotting those against the probability of values coming up based on the 1d00 roll.
Following that I looked up the probabilities for various die rolls on anydice.com and settled on 3d6 as giving a reasonable amount of variance.
Finally, I used the probability of doubles or trebles occurring to generate similar curves to those in the DMG.
I don't recall exactly how I figured those out but I suspect I probably just Googled and grabbed the first answer that looked right. For the purposes of post, I did a bit of digging around for one that explained how to get to the numbers; here's a good one, Probability for Dummies.
What is the probability of rolling doubles (not triples) on 3d6? This one is tricky. Let's break it down by first examining case one: the first two rolls match and third does not. The first roll can be anything (probability 1). The second roll must match the first (probability 1/6). The third roll must not match (probability 5/6, do you see this?). So to total probability for case one is 1 1/6 5/6 = 5/36.
Mr. Ekted then goes on to outline the remaining two possible outcomes and adds all three together to get a final probability.
For these purposes, I ended up with (rounding where appropriate):
- No doubles or trebles (one case): 56%
- 1 × 5/6 × 2/3 = 10/18
- Any double or treble: 44%
- 1st two rolls match: 1 × 1/6 × 5/6 = 5/36
- 1st and 3rd match : 1 × 5/6 × 1/6 = 5/36
- 2nd and 3rd match: 1 × 5/6 × 1/6 = 5/36
- all three match: 1 × 1/6 × 1/6 = 1/36
- Total: 5/36 + 5/36 + 5/36 + 1/36 = 16/36
- Three doubles or trebles, eg. 1, 2, or 3: 22%
- Half the total of all doubles and trebles
- Two doubles or trebles, eg. 4 or 5: 11%
- Two thirds of that half
- One double or treble, eg. 6: 6%
- Half that figure again
The notebook notes were a bit rough around the edges so I threw the numbers into another lovely spreadsheet...
Of course it turned out the table I'd created by hand didn't follow the DMG curves as well as I thought they had (damn spreadsheets with their accurate graphing capabilities) so I reworked it slightly with a Mark #2 version (pictured) and tried to line the curves as close as reasonable.
The Loot
While there's still a little variance between my table and the DMG's (remember, I've only been looking at the mean values here), the majority of rolls require just 3d6 - no more 1d00 then checking the table for an indeterminate number of d6s!
A downside is that CR11 creatures and greater are far more likely to have platinum pieces about their person but you can always use the coin conversion rate to mix it up a bit...
100 CP = 10 SP = 5 EP = 1 GP = 1/10 PP
Finally, the loot type table. Reusing the same 3d6 roll appealed so to allow a DM to take their three dice and check the numbers directly against the left side for mundane items, or if on a double or treble, against the right side for something a little more exotic.
None of my players have found an Ettin with a bureau yet but surely it's just a matter of time...
NB: This is an updated version of yesterday's article after I played around a little more with the numbers. (22 July 2018)